Description of the intrinsic spin Hall effect database
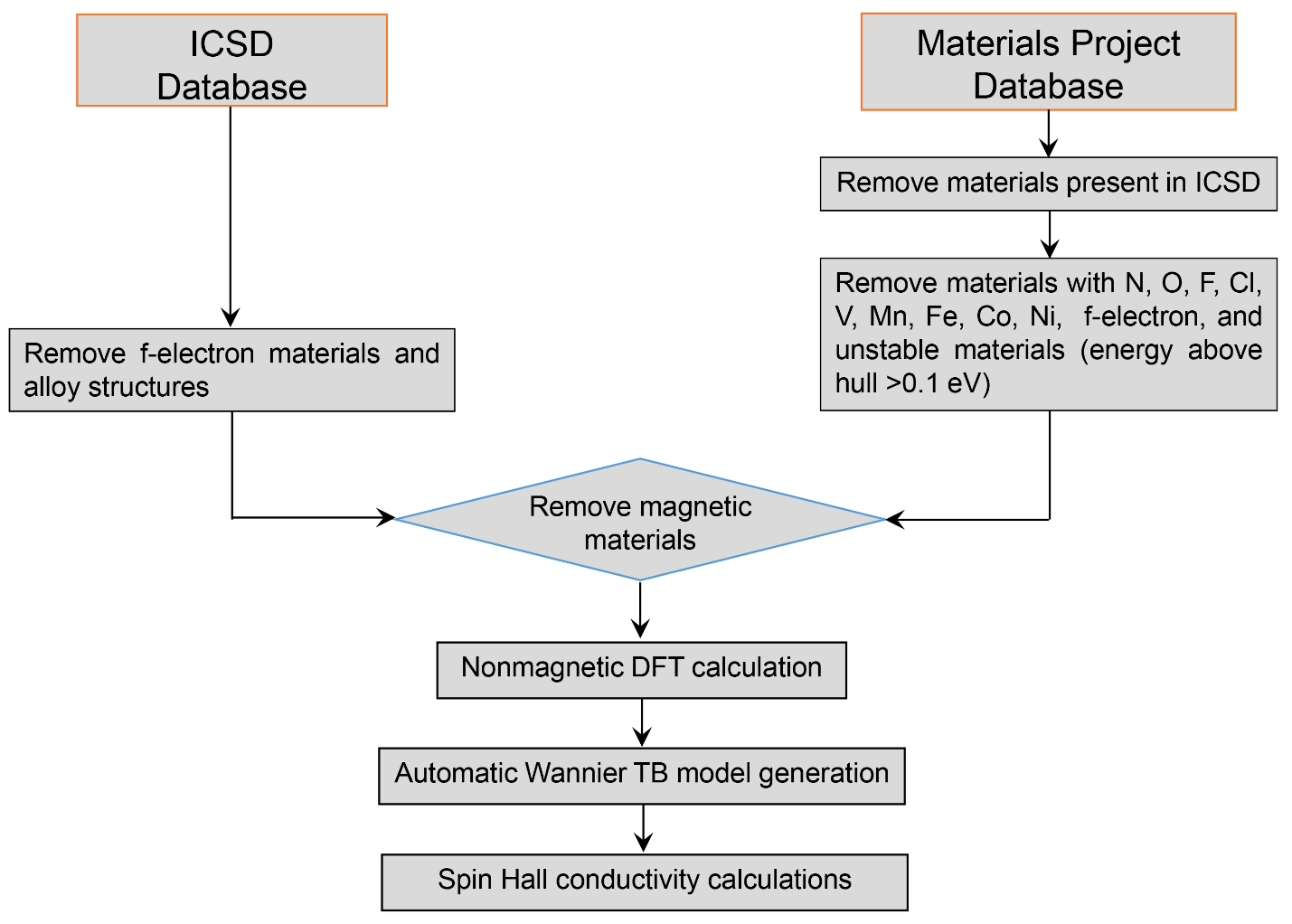
This database includes the calculated intrinsic spin Hall conductivities for over 8668 non-magnetic crystals. All the results in this database were obtained by following the work flow shown below, with the input from Materials Project and ICSD. The DFT calculations and automatic Wannier function generations were performed by the code of FPLO.
Within linear response, the spin current $J_i^k$ generated by an applied electrical field $E_j$ is described by $J_i^k=σ_{ij}^k E_j$, where $i$ corresponds to spin current flow direction and $k$ is its spin-polarization and $σ_{ij}^k$ is a 3x3x3 SHC tensor with 27 elements. According to crystal symmetries, we made four categories for the spin current: Type-I: traditional spin Hall effect with the electric field, spin current flow direction and the spin-polarization of the spin current are all perpendicular to each other, corresponding to nonzero $σ_{ij}^k (i\neq j\neq k )$; Type-II: spin current flowing in the direction transverse to the electric field with spin-polarization parallel with the spin current direction, corresponding to $σ_{ij}^i (i≠j)$; Type-III: spin current flowing in the direction of electric field, corresponding to nonzero $σ_{jj}^i$ (including $i≠j$ and $i=j$ ). Type-IV: spin polarization of spin current parallel to applied electrical field, corresponding to $σ_{ij}^j (i≠j)$.
The existence and magnitude of non-orthogonal spin current can be also obtained by rotating applied electrical field. With electrical field rotating in the space, the non-orthogonal spin current can appear in any space groups except $m\overline{3}m$. For the type-II spin current we first looped over electric field directions $\hat{\mathrm{\textbf{E}}}$ (here $\hat{\mathrm{\textbf{E}}}$ denotes a unit vector), thus obtaining $J_i^k=σ_{ij}^k\hat{E}_j$ for every $\hat{\mathrm{\textbf{E}}}$. Then we looped over directions $\hat{\mathrm{\textbf{d}}}$ perpendicular to $\hat{\mathrm{\textbf{E}}}$ and for each direction calculated the spin current flowing along this direction with spin-polarization along this direction as $s=J_i^k\hat{d}_i\hat{d}_k$. For type-III spin current we obtained the longitudinal spin current as $j_{||}^k= J_i^k\hat{E}_i$. This corresponds to a spin current with magnitude given by $|\mathrm{\textbf{j}}_{||}|$ and spin-polarization in the direction $\mathrm{\textbf{j}}_{||}$ direction. The tensor elements for type-IV spin currents were obtained in a similar way with that in type-III. We note that an alternative approach for obtaining the type-II to type-IV spin current is to loop through rotations of the coordinate system and identify the rotations giving the largest tensor elements corresponding to the type-II to type-IV spin currents. The two SHC tensors before and after rotation are related by $$σ_{ij}^k = \sum_{lmn} D(R)_{il}D(R)_{jm}D(R)_{kn}σ_{lm}^n,$$ where the 3x3 rotation matrix $\hat{D}$ can be constructed from three joint rotation with respect to x, y, and z axis in the way of $\hat{D} = \hat{D}(R_x)\hat{D}(R_y)\hat{D}(R_z)$.